作者：Resonare
版本：v1.0
说明：本笔记用于系统梳理数学分析（实变函数论初步）核心内容，兼顾直觉理解、形式化推导与常见题型。

后续不定期更新，半年内应该可以完成。

第0章：为什么要做分析

“数学分析不是算术的延伸，而是思维的锻造。”

还记得高中数学老师在课堂上说过，我们现在所学的数学本质上还是算数，当时的大家一笑过。

回过头来品味高中数学，我们学到的导数，所谓的“极值点偏移”，有些人会拿来在课堂上装的洛必达法则，那时候我们只是在机械的计算，此为“算数”。

进入大学之后，我们开始接触分析学，分析学最大的特点就是严谨和完备，这才叫做“分析”。

以陶哲轩《实分析》和华东师大《数学分析》为母本（Copy），加以作者本人的理解整理为

0.1 什么是分析

数学分析，笔者看来是将注重分析的实分析与注重计算规则的微积分的有机结合，既然是分析，我们在之后的讲解中不仅仅会讲述注重于计算技巧的微积分，也会穿插实分析相关的内容。

实分析，是关于实数、实数列、实数级数以及实值函数的分析。实分析是微积分学的基础，而微积分是我们在处理函数时用到的计算工具。

在后面，我们主要讨论以下几点

1.什么是实数？是否存在最大的实数？

2.什么是极限，什么样的序列有极限？

3.什么是函数，函数的性质分别是什么，具有什么意义？

0.2 为什么要分析

我们先来看一个例子：

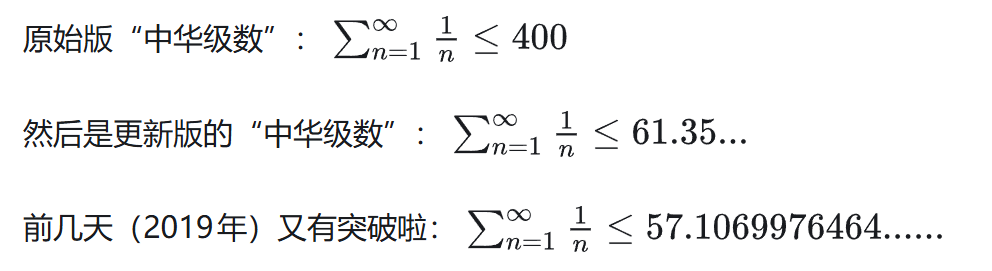
调和级数求和在著名民科的手里，变成了收敛的，而且随着时间改变收敛于不同的值。

还有被民科每天证明的歌德巴赫猜想：

学习分析的主要目的就是为了正确解决以上问题，了解这些法则在什么情况下是适用的，这些法则的使用有什么限制条件。而且对于工科同学，学习分析学还可以帮助你更好的解决实际问题，比如物体的表面不是一个完美的球体，甚至是不连续的情况，我们都可以从分析学中找到对应的工具将他们拆解为我们已知的模型。

你们都比我聪明，只是妄自菲薄而已！——YAU